Les problèmes de constructions géométriques, dites 'à la règle et au compas' remontent (au moins) à l'antiquité grecque.
Les postulats géométriques des Éléments d’Euclide ont fixé, pour les grecs anciens, quelles étaient les règles permises pour effectuer des constructions géométriques. Une construction effectuée à la règle et au compas respecte les règles du jeu. Une construction qui est basée sur d’autres outils que la règle et le compas ne respecte pas les règles du jeu.
Et ces règles du jeu quelles sont-elles ?
On dispose dans le plan :
- De deux points distincts disons A et B, qui déterminent l'unité de longueur.
- D'un compas
- D'une règle non graduée
Une doite est déterminée par deux points distincts et un cercle est déterminé par son centre et un point de la circonférence (donc un rayon).
Avec cela on peut construire :- Des figures géométriques, telles :
- Des médiatrices de segments
- Des bissectrices d'angles
- Des cercles, comme le cercle circonscit à un triangle
- Des angles de mesure donnée (60°,45°,108°, etc)
- Des polygones réguliers (carré, hexagone, pentagone, etc.)
Un calcul thérorique montre que le côté du pentagone régulier convexe inscrit dans un cercle de rayon 1 est :
$$\frac{\sqrt{50+10\sqrt{5}}}{10}$$Si on a construit ce nombre , c'est à dire un segment dont la mesure est ce nombre, il suffit de régler l'ouverture du compas avec ce segment et de reporter 5 fois sur le cercle unité. Lui-même construit comme cercle de centre A et de rayon [AB].
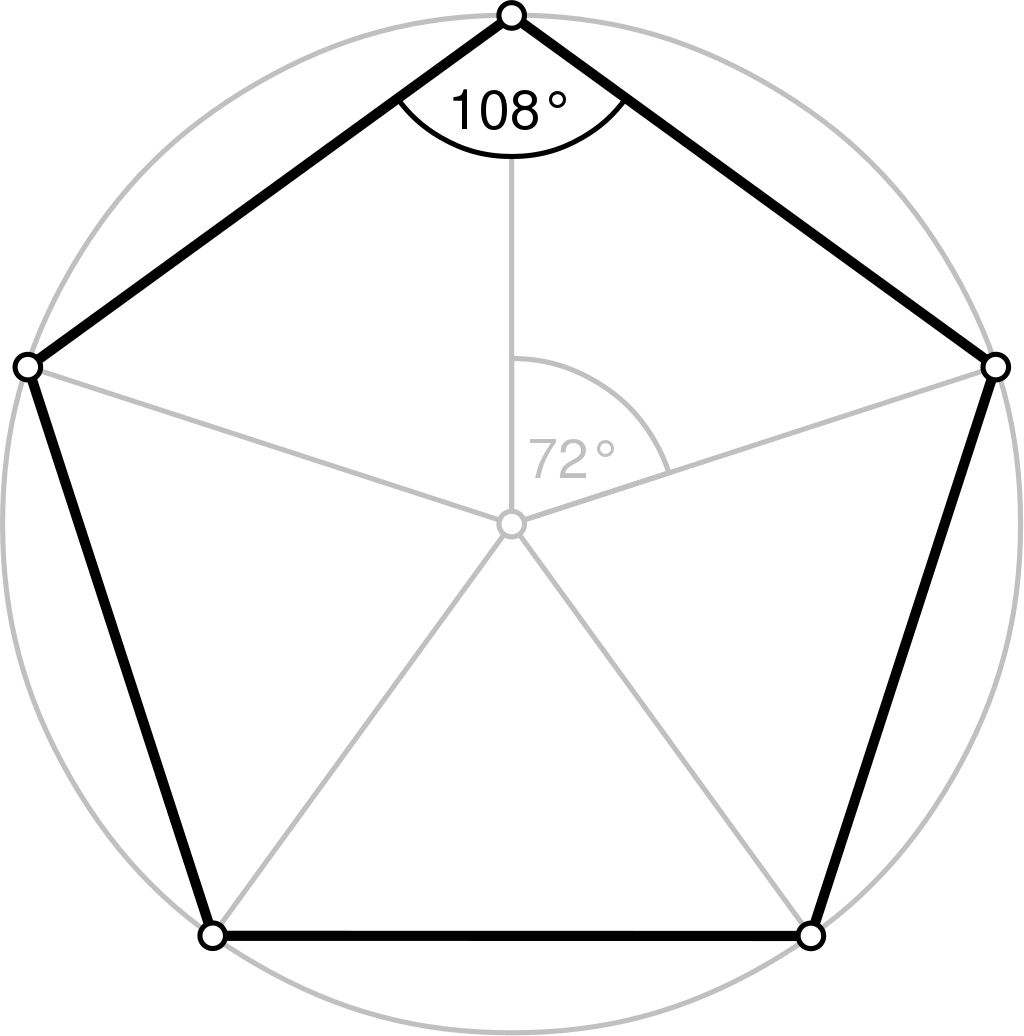
Inversement si on a construit le pentagone, on a construit le nombre ci-dessus.
Par ailleurs la construction d'un angle, par exemple de 108° = 3π/5 rd permet de construire le pentagone, par report des angles au compas, donc le nombre.
- Des points de façon récursive. Les points de départ A et B sont supposés construits, tout point obtenu comme intersection de droites et de cercles construits eux-mêmes construits au sens précédent, reçoit le qualificatif de 'construit'.
- Enfin des nombres. Les nombres sont assimilés à des longueurs de segments construits. Ainsi par exemple pour construire le nombre √2 on construit un carré de côté 1 sur le segment [AB] d'origine, la diagonale de ce carré a la propriété voulue.