Voici donc quelques constructions classiques :

Construction de points

Nous construisons ici le symétrique d'un point par rapport à un autre point.

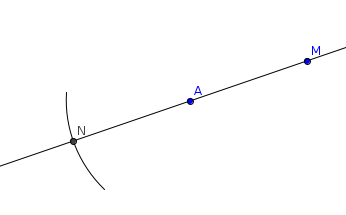
Nous voulons tracer le symétrique de M par rapport à A.

• Nous traçons la droite (AM).
• Nous traçons le cercle de centre A et de rayon AM.
• Soit N le point d'intersection de la droite et du cercle autre que M

N est le point cherché.

Nous construisons maintenant le symétrique orthogonal d'un point M par rapport à une droite Δ.

• Tracer un cercle de centre M et de rayon R suffisamment grand pour pour qu'il coupe Δ en deux points A et B.
• Tracer le cercle de centre A et de rayon R.
• Tracer le cercle de centre B et de rayon R.
• Les deux cercles précédents se coupent en M et un autre point N.

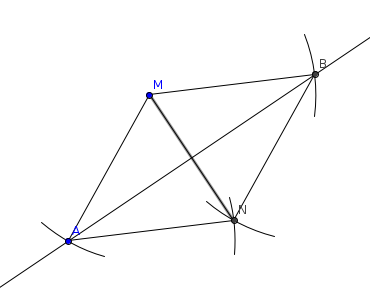
La figure MANB est un losange.

Ses deux diagonales sont donc perpendiculaires et se coupent en leur milieu.

Construction de figures

Médiatrice d'un segment

Par Ixnay — Travail personnel, Domaine public, https://commons.wikimedia.org/w/index.php?curid=1888648

Bissectrice d'un angle

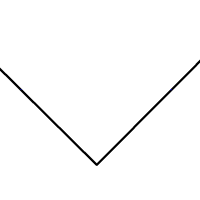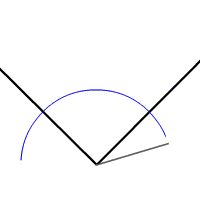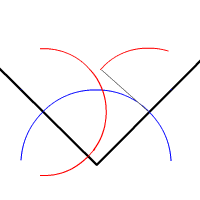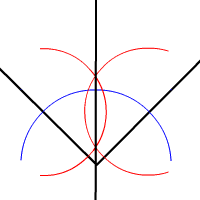
Par Ixnay — Travail personnel, Domaine public, https://commons.wikimedia.org/w/index.php?curid=1888648

Perpendiculaire à une droite passant par un point donné

Par I, Alcandre, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2427340

On utilise simplement la construction de la médiatrice ci-dessus.

Parallèle à une droite passant par un point donné

On cherche la droite parallèle à la droite Δ bleue passant par le point C.

1. Tracer un cercle de centre C et rayon suffisamment grand pour qu'il coupe Δ en deux points distincts E et F.
2. Tracer le cercle C₁ de centre F et de rayon CE.
3. Tracer le cercle C₂ de centre C et de rayon EF.
4. Soit G le point d'intersection de C1 et C2 tel que CEFG soit convexe.

Alors CEFG est par construction un parallèlogramme, la droite (CG) rouge est donc la droite cherchée.

Construction d'angles

On fabrique ici un angle de 108° par un pentagone régulier inscrit, par la méthode de Ptolémée.

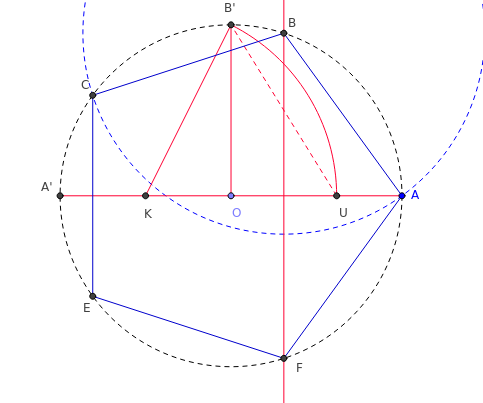
Nous reprenons le travail de Patrice Debart.

Construction à partir d'un sommet A, situé à l'extrémité d'un diamètre du cercle circonscrit.

Tracer le cercle (C₁) de centre O, passant par A. On choisira comme unité le rayon du cercle. Placer un diamètre [AA’] et un rayon [OB’], perpendiculaire à [AA’]. K est le milieu de [OA’], le cercle de « Ptolémée » de centre K et de rayon KB’ coupe [OA] en U. OU/OA = (φ nombre d'or) : le point U partage le rayon [OA] en moyenne raison. La longueur du côté du pentagone est égale à B’U.

La médiatrice de [OU] coupe le premier cercle (C₁) aux points B et F qui sont deux sommets du pentagone. Le cercle de centre B passant par A recoupe () en C. Le symétrique D de C par rapport à (AA’) termine la construction du pentagone. La corde [AB] est donc le premier côté du pentagone régulier convexe ABCDE.

Construction de nombres

Voici un exemple simple, la construction de √3 :

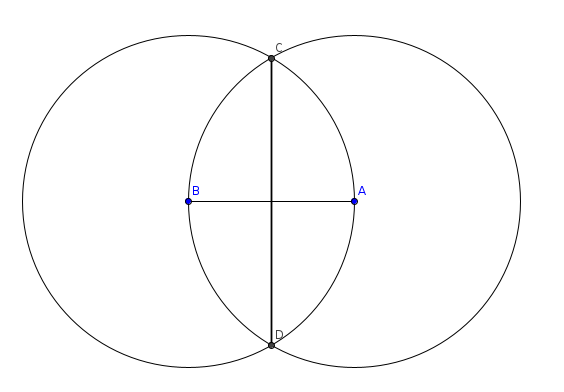
A partir de l'unité (segment [AB]), nous fabriquons un triangle équilatéral ABC, dont la hauteur vaut √3/2.

Il suffit de doubler cette longueur.

Si AB vaut 1, alors CD vaut √3.