Les 'nombres', tels que vus par les Anciens, correspondaient aux longueurs des segments. D'une certaines façons on ne fait guère mieux aujourd'hui en parlant de 'droite réelle'.
Il y a quand même une restriction, ils ne considéraient pas de nombres négatifs.
Nous allons voir comment, en particulier, tous les rationnels (positifs, donc) sont constructibles.
Sommes
Pour former AB+CD, on reporte avec le compas, sur la droite AB, un segment BE, E ∉ ]A,B[, de longueur CD. Le segment [AE] a la longueur voulue.
A partir de AB=1 on peut ainsi construire 2,3, et tous les entiers positifs.Produits
Si a et b sont deux constructibles, alors on sait construire le produit a×b :
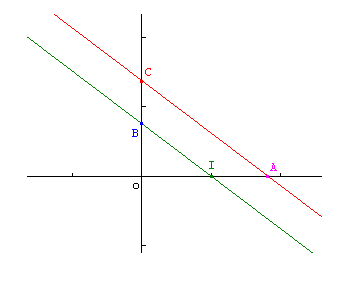
On considère le point A (a,0), et B(0,b). On trace la parallèle à (BI) passant par A, qui coupe l'axe des ordonnées en C.
D'après le théorème de Thalès, OC/OB=OA/OI, ce qui donne OC=ab.
Quotients
Si a et b sont deux constructibles, avec b non nul, alors on sait construire le quotient a/b :
On considère les points A(a,0) ; B(b,0) et C(0,1). On trace la parallèle à (BJ) passant par A, qui coupe l'axe des ordonnées en C.
D'après le théorème de Thalès, OC/OJ=OA/OB, d'où OC=a/b.
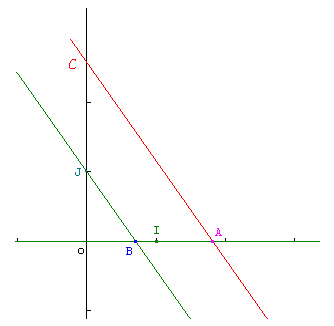
Il en résulte immédiatement que tous les rationnels positifs, quotients de deux entiers naturels, sont constructibles.
Racines carrées
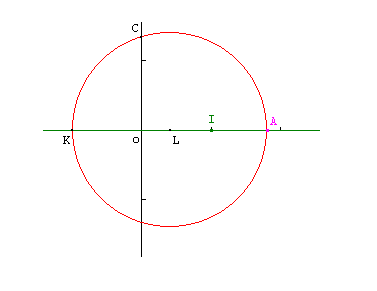
Soit $A$ de coordonnées $(a,0)$ et $K$ de coordonnées $(-1,0)$. On commence par déterminer, à la règle et au compas, $L$ le milieu de $[AK]$, qui a donc pour coordonnées $((a-1)/2,0)$.
Puis on trace le cercle de centre $L$ passant par $A$ (et $K$). Il coupe l'axe des ordonnées en $C$.
En appliquant le théorème de Pythagore au triangle $COL$, rectangle en $O$, on a : $$OC^2=CL^2-OL^2.$$
Puisque $CL=AL=(a+1)/2$ et $OL=(a-1)/2$, on obtient en développant $OC^2=a$ et donc $OC=\sqrt a$.
Synthèse
Même si on ne sait pas construire explicitement le nombre :
$$p=\frac{\sqrt{50+10\sqrt{5}}}{10}$$ Voir paragraphe précédent.On sait a priori qu'il est constructible :
- 5 est entier donc constructible.
- √5 est constructible comme racine carrée d'un constructible.
- 10 est entier donc constructible.
- 10√5 est constructible comme produit de deux constructibles.
- 50+10√5 est constructible comme somme de deux constructibles.
- $\sqrt{50+10\sqrt{5}}$ est constructible comme racine d'un constructible.
- p est constructible comme quotient de deux constructibles.
On peut bien sûr enchaîner les processus de construction pour obtenir des algorithmes, bien que dans de nombreux cas des méthodes plus simples existent.