Définitions
Soit X un ensemble quelconque. On dit que G est 'libre de base X' s'il existe une injection i:X$\hookrightarrow$ G, telle que pour toute application f:X→H de X dans un groupe H quelconque, il existe un unique homomorphisme $\hat{f}$:G→H tel que f=$\widehat{f}\circ$i. C'est à dire rendant commutatif le diagramme :
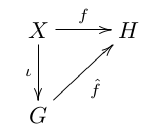
Remarquons pour commencer la similarité avec la base d'un espace vectoriel en algèbre linéaire. Une application linéaire (morphisme d'espaces vectoriels) est entièrement déterminée par les valeurs qu'elle prend sur les éléments d'une base.
Remarquons aussi que nous avons défini un objet mathématique par des propriétés, mais qu'à ce stade rien ne prouve qu'un tel objet existe. Nous allons donc le construire un peu plus loin. Par ailleurs pas plus que l'existence, l'unicité n'est évidente. Nous commencerons par ce point comme souvent en mathématiques nous allons établir l'unicité (à un isomorphisme près) d'un groupe libre. En outre X n'intervient que par son cardinal en ce sens que si X et Y sont deux ensembles équipotents, les groupes libres associés seront isomorphes.
Puisque X et Y ont même cardinal il existe des bijections α:X→Y et β:Y→X réciproques l'une de l'autre, c'est à dire que β$\circ$α=IdX et α$\circ$β=IdY.
La propriété universelle des groupes libres, nous assure alors l'existence de morphismes $\widehat{j\alpha}$:G→H, prolongeant jα:X→H, et $\widehat{i\beta}$:H→G prolongeant iβY→G. De sorte que nous ayons les deux carrés commutatifs.
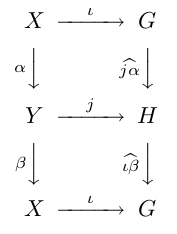
Ce qui entraîne un nouveau diagramme commutatif :

Or β$\circ$α=IdX et le diagramme suivant est commutatif :
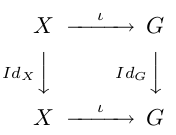
Il s'en suit d'après la propriété universelle du groupe libre que $\widehat{i\beta}$$\widehat{j\alpha}$=IdG.
On démontre de la même façon que $\widehat{j\alpha}$$\widehat{i\beta}$=IdH.
En définitive $\widehat{j\alpha}$ et $\widehat{i\beta}$ sont des isomorphismes réciproques l'un de l'autre.
A ce stade nous savons donc que si un groupe libre existe associé à un ensemble X, il est unique (à un isomorphisme près). S'il existe nous le noterons $\mathfrak{F}$(X).
Construction
Il est temps de passer à la construction de $\mathfrak{F}$(X), ce qui équivaudra à une attestation d'existence.
Commençons par 'symétriser' X, soit donc X-1 un ensemble équipotent à X et disjoint de X avec une bijection φX:→X-1.
Pour tout x de X nous notons x-1 l'élément φ(x). x-1 est donc en quelques sorte l'inverse 'formel' de x.
Nous posons maintenant $\overline{X}$=X∪X-1.
Nous appelons $\overline{X}$ l'alphabet du groupe libre.
Nous définissons les 'mots' de cet alphabet de façon récursive. Les mots sont en fait des chaînes de caractères appartenant tous à $\overline{X}$.- La chaîne vide '' est un mot.
- Si m est un mot alors m+'c' (concaténation de m avec la chaîne 'c' où c∈$\overline{X}$ est encore un mot.
Nous désignons par $\mathfrak{M}$(X) l'ensemble de tels mots.
Alors la 'concaténation' (m1,m2):→m1+m2 consistant à former une nouvelle chaîne en ajoutant un à un tous les caractères du mot m2 à la suite de ceux de m1, est une opération assurément associative admettant pour neutre la chaîne vide ''.
Nous introduisons maintenant sur $\mathfrak{M}$(X) une relation d'équivalence.
Un mot est 'irréductible' s'il ne comporte aucun 'motif' (sous-chaîne) du type 'xx-1' ou 'x-1x'. 'Simplifier' un mot consiste à ôter de ce mot tous les motifs de l'un de ces types. 'Réduire' un mot m signifie simplifier à répétition jusqu'à obtenir un mot irréductible r(m).
Nous définissons maintenant entre les mots, la relation m∼m' ssi r(m)=r(m'). Alors clairement ∼ est une relation d'équivalence.
On vérifie ensuite que ∼ est compatible avec la concaténation en se sens que si m1∼m'1 et m2∼m'2 alors (m1+m2)∼(m'1+m'2). Cela provient du fait que r(m1+m2)=r(r(m1)+r(m2)).
La concaténation (+) devient alors une loi de groupe. L'inverse de x1x2....xn étant xn-1...x2-1x1-1 (avec la convention (x-1)-1=x).
Posons pour tout élément x-1 de X-1 f(x-1)=f(x)-1. f est donc définie sur X.
Pour tout mot m=x1x2....xn nous posons f(m)=f(x1)f(x2)....f(xn), alors f est étendue à $\mathfrak{M}$(X) et vérifie f(m1m2)=f(m1)f(m2) et si m' est simplifié de m f(m')=f(m).
On en déduit que f est compatible avec ∼ et qu'on peut définir un homomorphisme $\widehat{f}$:$\mathfrak{F}$(X)→H par passage au quotient avec $\widehat{f}$(m)=f(m).
Il est clair que $\widehat{f}$ est entièrement déterminé par les valeurs de f sur les éléments de X.
Exemples
Le groupe libre associé à un singleton est tout simplement ℤ. $\mathfrak{F}$({x})={xn| n∈ℤ} avec la convention xn=xx...x (mot de n caractères tous égaux à x si n>0 ), xn=x-1x-1...x-1 (mot de n caractères tous égaux à x si n<0 ) et x0='' (chaîne vide).
De la même façon $\mathfrak{F}$({x,y}) correspond à l'ensemble des chemins joignant l'origine à chacun des points du plan à coordonnées entières (chemins dans le treillis ℤ×ℤ)