Nous rappelons que K désigne ici un corps commutatif. K est donc en particulier un anneau intègre.
K[X] désigne l'algèbre des polynômes à une indéterminée à coefficients dans K, qui est donc muni d'une structure d'espace vectoriel sur K et d'une structure additionnelle d'anneau intègre (revoir ce résultat).
- A=BQn+Xn+1(Sn)
- d°(Qn)≤n
Existence
Elle se fait par récurrence sur n.
Pour n=0 soit a0 le terme constant de A. Soit Q0 le polynôme constant a0/b0. On constate alors que A-BQ0 est un polynôme sans terme constant, donc factorisable par X. on peut donc mettre A-BQ0 sous la forme XS0.
Soit maintenant n fixé et supposons le théorème vrai pour tous polynômes et tout entier i≤n.
Effectuons d'abord la division suivant les puissances croissantes de A par B à l'ordre n : A=BQn+Xn+1Sn, puis effectuons la division suivant les puissances croissantes de Sn par B à l'ordre 0 : Sn=kB+XT. Par substitution on en déduit que : A=BQn+kBXn+1+Xn+2T. On peut donc prendre Qn+1=Qn+kXn+1 et Sn+1=T pour obtenir le théorème à l'ordre n+1.
Unicité
Supposons qu'on ait deux écritures :
A=BQ1,n+Xn+1S1,n
A=BQ2,n+Xn+1S2,n
avec d°(Q1,n)≤n et d°(Q2,n)≤n
Posons Qn=Q1,n-Q2,n et Sn=S1,n-S2,n.
De sorte que 0=BQn+Xn+1Sn< avec d°(Qn)≤n.
Comme on a supposé que b0≠0, X ne figure pas parmi les facteurs irréductibles de B, donc Xn+1 est premier avec B. Mais d'après l'égalité BQn=-Xn+1Sn Xn+1 divise BQn, donc Xn+1 divise Qn, ce qui contredit l'hypothèse sur le degré de Qn, sauf si Qn=0 qui entraîne alors Sn=0.
Algorithme
De fait la démonstration d'existence décrit l'algorithme, comme pour la division euclidienne, sauf qu'on cherche à faire disparaître les termes de plus bas degré au lieu de ceux de plus haut degré.
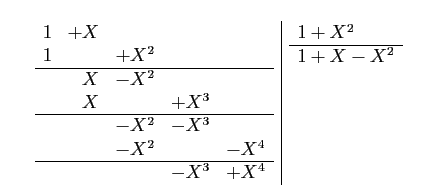
Voici par exemple l'opération correspondant à A=X+1 et B=X2+1, à l'ordre n=2.