Soient H et K deux sous-groupes d'un groupe G. On pose HK={xy | x∈H et y∈K}.
Illustrons par un exemple :
Soit S3 le groupe symétrique des permutations de l'ensemble {1,2,3}. Ce groupe est composé de 6 éléments. L'identité, trois transpositions, et deux cycles d'ordre 3. Voici sa table.
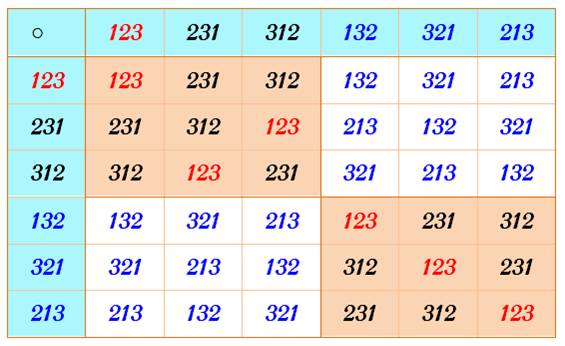
Prenons H={123,132} et K={123,321}
Alors HK={123,132,321,231} et KH={123,132,321,312}
On voit donc que HK≠KH et que ni l'un ni l'autre n'est un sous-groupe de S3, car l'ordre d'un tel sous-groupe doit diviser l'ordre de S3 c'est à dire 3!=6.
HK est ainsi a priori une simple partie de G. Nous allons maintenant trouver une condition suffisante pour que ce soit un sous-groupe de G.
H et K étant comme il est dit plus haut, une condition nécessaire et suffisante pour que HK soit un sous-groupe de G est que HK=KH.
- On suppose que HK est un sous-groupe de G. Soit x dans HK, son inverse x-1 est encore dans HK.
Ainsi ∃(h,k)∈H×K | x-1=hk on a alors x=(hk)-1=k-1h-1∈KH.
Donc HK⊆KH.
Soit de même y∈KH alors y=kh avec k∈K et h∈H. y-1=h-1k-1 est dans le sous-groupe HK, donc également son inverse y. Il en résulte que KH⊆HK, donc KH=HK. -
On suppose réciproquement que HK=KH.
Montrons que HK est un sous-groupe de G.
soi x=hk et y=h'k' dans HK. Alors y-1x=k'-1h'-1hk. k'-1 est dans K et h'-1 est dans H. En utilisant KH=HK il existe un couple (h",k")∈H×K tel que (k'-1)h'-1h=h"k" On peut donc écrire y-1x=h"k"k avec h"∈H et k"k ∈K. Il en découle que y-1x∈HK, ainsi HK est un sous-groupe de G.
Dans les hypothèses ci-dessus. HK est le plus petit sous-groupe de G contenant H et K. C'est donc sous-groupe engendré le sous-groupe engendré par H∪K. En outre HK contient H∩K comme sous-groupe.
En effet tout sous-groupe contenant H et K doit contenir, par stabilité tout produit hk avec h dans H et k dans K. Le second point est évident.
Nous allons maintenant nous concentrer sur le cas où H∩K={1}.
Si H∩K={1} tout élément x de HK s'écrit de façon unique x=hk avec h∈H et k∈K.
Supposons en effet hk=h'k' multiplions par h-1 à gauche et par k'-1 à droite. Il vient kk'-1=h-1h'.
Dans cette égalité le membre de gauche est dans K et le membre de droite est dans H, les deux membres sont donc égaux à 1. Il en résulte que k'=k et h'=h.
Si H∩K={1} et si H et K sont finis, alors HK est fini et card(HK)=|H|.|K|
Cela résulte immédiatement du point précédent.
Supposons maintenant que les conditions suivantes soient réalisées :
- H et K sont des sous-groupes de G
- H∩K={1}
- G=HK
- hk=kh ∀h∈H, ∀k∈K
Il est clair que dans ce cas HK=KH=G.
A tout x=hk de G avec h∈H et k∈K nous associons le couple (h,k)=φ(x) de H×K.
Si y=k'h' on a φ(xy)=φ(hkh'k')=φ(hh'kk')=(hh',kk')=(h,k).(h',k').
Sous les hypothèses du théorème précédent on dit que G est le 'produit direct' de H par K.
Dans le cas commutatif la condition iv est toujours réalisée. On retrouve ainsi par exemple la notion de sous-espaces vectoriels supplémentaires.
Remarque : Dans le théorème précédent, les trois premières conditions étant vérifiées une condition suffisante pour que iv soit vérifiée est que H et K soient tous deux distingués dans G.
En effet pour tout h∈H et tout k∈K on a :
$$H\ni h\left ( kh^{-1}k^{-1} \right )=\left ( hkk^{-1} \right )k^{-1}\in K$$
donc $hkh^{-1}k^{-1}=1$ d'après ii et par suite hk=kh.