Définition
On appelle 'suite de composition' d'un groupe G, toute chaîne finie décroissante du type :
G=G0$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$......Gn-1$\vartriangleright$Gn={1}
On rappelle que le symbole Gi$\vartriangleright$Gi+1 signifie que Gi+1 est un sous-groupe distingué de Gi.
En outre on suppose que chacun des groupes quotients Gi/Gi+1 est commutatif
Le nombre n de quotients est appelé la 'longueur' de la suite.
La suite est dite 'strictement décroissante' si Gi≠Gi+1 ∀i 0≤i≤n-1.
Les exemples qui suivent sont empruntés à François Dumas.
Exemple 1
Soit S4 le groupe symétrique (ex n°7) d'ordre 4, c'est à dire le groupe des 24 permutations de {1,2,3,4}.
A4 désigne le groupe alterné d'ordre 4, donc sous-groupe de S4 (cf ex 11)
- e désigne la permutation identique.
- a échange 1 et 2 ainsi que 3 et 4.
- b échange 1 et 3 ainsi que 2 et 4.
- c échange 1 et 4 ainsi que 2 et 3.
- On désigne par V l'ensemble {e,a,b,c}, dont on vérifiera que c'est un sous-groupe de A4 et de S4(Vierergruppe de Klein).
- On désigne par H l'ensemble {e,a} dont on vérifiera que c'est un sous-groupe de V, A4 et S4.
Nous laissons au lecteur le soin de vérifier que :
- S4$\vartriangleright$ A4$\vartriangleright$V$\vartriangleright${e}
- S4$\vartriangleright$ A4$\vartriangleright$V$\vartriangleright$H$\vartriangleright${e}
Exemple 2
Considérons le groupe diédral D4={e,r,r2,r3,s,sr,sr2,sr3} où r est la rotation d'angle π/2 et s la symétrie d'axe x'Ox.
On vérifiera que les sous ensembles suivants sont bien des sous-groupes de D4.
- V1={e,r2,s,sr2}
- V2={e,r,r2,r3}
- V3={e,r2,sr,sr3}
- H1={e,s}
- H2={e,sr2}
- H3={e,r2}
- H4={e,sr3}
- H5={e,sr}
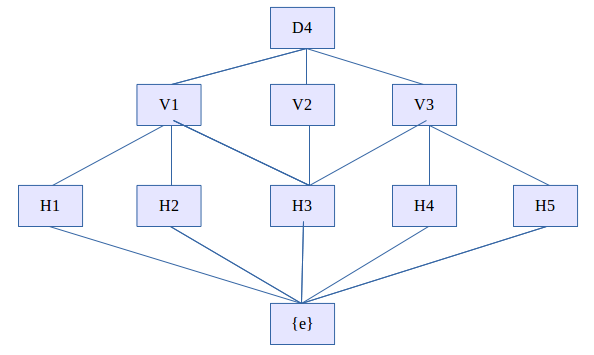
Tout chemin de D4 à {e} à 4 sommets dans ce diagramme est une suite de composition. Nous laissons au lecteur le soin de le vérifier.