Nous rappelons que K désigne ici un corps commutatif.
K[X] désigne l'algèbre des polynômes à une indéterminée à coefficients dans K, qui est donc muni d'une structure d'espace vectoriel sur K et d'une structure additionnelle d'anneau intègre (revoir ce résultat).
Voici le résultat principal :- A=BQ+R
- d°(R)<d°(B)
La démonstration de l'existence se fait par récurrence sur le degré de A.
Le théorème est évidemment vrai pour d°(A)<d°(B) auquel cas Q=0 et R=A.
Supposons donc d°(A)≥d°(B) posons d°(A)=m et d°(B)= n avec m≥n. Soit d=m-n alors d≥0. On considère le monôme Xd. Il est clair qu'on peut trouver a∈K tel que A-aXdB ait pour degré m-1. Il suffit de prendre pour a le quotient du coefficient dominant de A par celui de B.
On applique alors l'hypothèse de récurrence à A'=A-aXdB. Il existe donc des polynômes Q' et R' tels que : A-aXdB=Q'B+R' soit encore A=(aXd+Q')B+R'.
On a d°(R')<D°(B) par hypothèse de récurrence. Il suffit donc de prendre Q=aXd+Q' et R=R'.
Remarquons au passage que la démonstration fournit en même temps l'algorithme de résolution.
Passons maintenant à l'unicité.
Supposons A=BQ+R = BQ'+R', avec d°(R)<d°(B) et d°(R')<d°(B) alors il vient B(Q-Q')=R-R'. Mais si Q n'est pas égal à Q' le polynôme de gauche est de degré au moins égal à celui de B tandis que celui de droite est de degré strictement inférieur à celui de B. Donc nécessairement Q=Q' et par suite R=R'.
En effet la division euclidienne de P par X-a donne P=(X-a)Q+k où k est une constante (polynôme de degré <1).
Compte tenu de ce résultat on a P(a)=(a-a)Q(a)+k.
De sorte que a racine de P ⇔ k=0.
Algorithme de détermination
On pose une sorte de division avec potence :
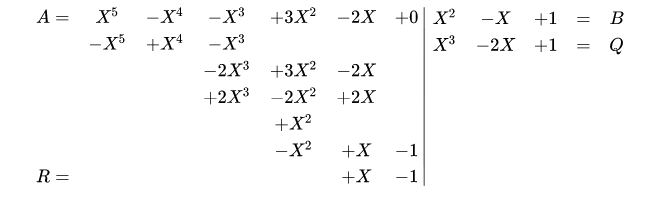
Représentations en informatique
Voici deux exemples de division euclidienne avec le langage julia 1.6 et le package Nemo :