Pour tout idéal J de B l'image réciproque h-1(J) est un idéal de A.
Pour tout idéal I de A, l'image h(I) est un idéal de l'anneau f(A) (mais pas forcément de B !)
Pour tout idéal I de A, l'image h(I) est un idéal de l'anneau f(A) (mais pas forcément de B !)
On voit déjà que h-1(J) est un sous-groupe de A puisque h est en particulier un homomorphisme de groupes. Soit alors x∈h-1(J). Soit a un élément quelconque de A, on a h(ax)=h(a)h(x), or h(x)∈J⇒h(a)h(x)∈J. Donc h(ax)∈J, et
ax∈h-1(J), CQFD.
Si I est un idéal de A h(I) est un sous-groupe additif de B. soit b∈h(A) alors b=h(y) avec y∈A. Si x∈h(I), ah(x)=h(y)h(x)=h(xy)∈f(I).
Il en résulte en particulier que :
Si I est un idéal de A h(I) est un sous-groupe additif de B. soit b∈h(A) alors b=h(y) avec y∈A. Si x∈h(I), ah(x)=h(y)h(x)=h(xy)∈f(I).
Dans les hypothèses du résultat précédent. h-1({0}) est un idéal de A.
Cela résulte simplement du fait que {0} est un idéal de B.
f étant un morphisme d'anneaux. Il y a équivalence entre :
- f est injectif
- Ker(f)={0}
En effet f(a)=f(b) ⇔ f(a)-f(b)= f(a-b)=0 ⇔ a-b∈ Ker(f).
Il résulte de ceci que :
Tout morphisme d'anneaux non nul défini sur un corps est nécessairement injectif (est un monomorphisme).
En effet si f est un tel morphisme défini sur le corps K, son noyau est un idéal de K, d'après l'exemple 2 ce ne peut donc être que {0} ou K. Puisque ce n'est pas K c'est {0}. f est donc injectif en vertu du résultat précédent.
h-1({0}) se note Ker(h) et est appelé 'noyau' de h.
Si A est l'anneau de toutes les fonctions définies sur ℝ et à valeurs dans ℝ et h l'endomorphisme f:→h(f)=f(0) alors Ker(h) est l'ensemble des applications qui s'annulent en 0.
h(A) est un sous-anneau de B appelé 'image' de h et noté Im(h).
Cela résulte simplement de ceci.
On a alors un théorème d'isomorphisme.
Soit h:A→B un homomorphisme d'anneaux. Alors h induit un isomorphisme h:A/Ker(h):→Im(h)
Cela résulte du fait que h(x)=h(x')⇔x-x'∈Ker(h), et que h définit une surjection de A sur son image Im(h)⊆B. h est ainsi défini par h(x)=h(x).
On peut en fait raffiner ce résultat pour obtenir la 'propriété universelle de l'anneau quotient'.
Soit A un anneau commutatif unitaire, I un idéal de A et p la surjection canonique A:→A/I. Pour tout anneau commutatif unitaire B et tout morphisme h:A→B tel que I⊆Ker(h), il existe un unique morphisme H de A/I dans B tel que h=H$\circ$p.
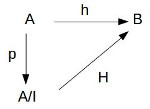
De plus h surjectif⇔H surjectif et I=Ker(h)⇔H injectif.

De plus h surjectif⇔H surjectif et I=Ker(h)⇔H injectif.
La démonstration ne présente aucune difficulté, il suffit d'appliquer les définitions et les propriétés précédentes.
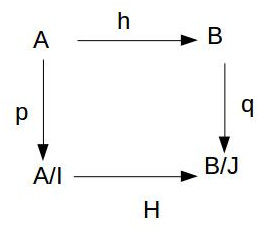
Dans la même veine nous avons également le 'lemme fondamental de factorisation' :Soit A un anneau commutatif unitaire, I un idéal de A, p la surjection canonique p:A→A/I.
Soit B un anneau commutatif unitaire, J un idéal de B, q la surjection canonique q:B→B/J. Alors pour tout morphisme h:A→B vérifiant h(I)⊆J, il existe un unique morphisme H:A/I→B/J tel que H$\circ$p=q$\circ$h