Nous suivons ici le plan de François Dumas.

Définition

Soit G un groupe et Σ:G=G0$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$......Gn-1$\vartriangleright$Gn={1} une suite de composition strictement décroissante. On dit que Σ admet un 'raffinement propre' lorsqu'il existe i : 1≤i≤n-1 et un sous-groupe K: Gi$\vartriangleright$K$\vartriangleright$Gi+1 avec K≠Gi et K≠Gi+1.

Remarque

Comme Gi+1$\vartriangleleft$Gi, tout sous groupe K tel que Gi+1⊂K⊂Gi vérifie Gi+1$\vartriangleleft$K. En conséquence :

Dire que Σ n'admet pas de raffinement propre signifie que ∀i 1≤i≤n-1 on ne peut pas trouver de sous-groupe K tel que Gi+1⊂K$\vartriangleleft$Gi, c'est à dire que Gi+1 est normal maximal dans Gi.
Nous donnons maintenant un lemme :

Soit G un groupe et Σ:G=G0$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$......Gn-1$\vartriangleright$Gn={1} une suite de composition de G, strictement décroissante.

Les assertions suivantes sont équivalentes:

  1. Σ est sans raffinement propre.
  2. Gi+1 est normal maximal dans Gi ∀i 0≤i≤n-1
  3. Gi/Gi+1 est un groupe simple ∀i 0≤i≤n-1

L'équivalence de i. et ii. résulte de la remarque précédente.

Rappelons d'abord que tout sous-groupe H normal de Gi/Gi+1 est de la forme K/Gi+1 où K est un sous-groupe normal de Gi contenant Gi+1 (revoir ce point). Alors :

Gi/Gi+1 simple ⇔ Gi/Gi+1≠{1} et si H$\vartriangleleft$Gi/Gi+1 alors H={1} ou H=Gi/Gi+1⇔ Gi≠Gi+1 et si Gi+1⊆K$\vartriangleleft$Gi alors K=Gi+1 ou K=Gi.

D'où l'équivalence de ii. et iii.

Une suite de composition satisfaisant l'une des trois conditions équivalentes du lemme ci-dessus s'appelle une 'suite de Jordan-Hölder' de G.

Exemples

  1. S5 désigne le groupe symétrique d'ordre 5 ex 7. A5 le groupe alterné ex n°11. La suite S5$\vartriangleright$A5$\vartriangleright${1} est de Jordan-Hölder car S5/A5 qui est d'ordre 2 est simple, et A5/{1}≅A5 est simple aussi (revoir).
  2. On reprend l'exemple 1 de cette page. La suite S4$\vartriangleright$A4$\vartriangleright${1} n'est pas de de Jordan-Hölder car A4 n'est pas simple.
    • Elle admet pour raffinement propre la suite S4$\vartriangleright$A4$\vartriangleright$V$\vartriangleright${1} qui n'est pas de Jordan-Hölder car V≅V/{1} n'est pas simple.
    • Elle admet pour raffinement propre la suite S4$\vartriangleright$A4$\vartriangleright$V$\vartriangleright$H$\vartriangleright${1}
      • qui est de Jordan-Hölder car V/H est d'ordre 2 donc simple tout comme H/{1}.
  3. Soit G le groupe cyclique G=ℤ/24ℤ. Dans G nous considérons les sous-groupes engendrés.
    • G2=<12>
    • G3=<8>
    • G4=<6>
    • G6=<4>
    • G8=<3>
    • G12=<2>

    On a donc le diagramme suivant où les flèches représentent des inclusions :

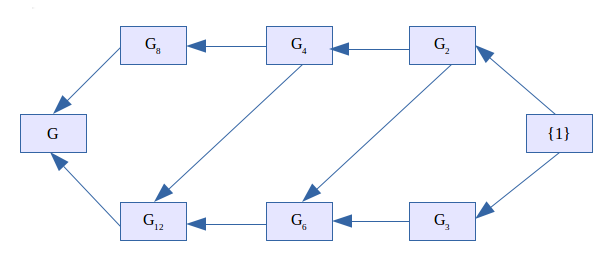
    On obtient 4 suites de Jordan-Hölder :

    • G$\vartriangleright$C12$\vartriangleright$C6$\vartriangleright$C3$\vartriangleright${1}
    • G$\vartriangleright$C12$\vartriangleright$C4$\vartriangleright$C2$\vartriangleright${1}
    • G$\vartriangleright$C12$\vartriangleright$C6$\vartriangleright$C2$\vartriangleright${1}
    • G$\vartriangleright$C8$\vartriangleright$C4$\vartriangleright$C2$\vartriangleright${1}

  4. Le groupe additif ℤ n'admet aucune suite de Jordan-Hölder.

    Raisonnons par l'absurde et supposons qu'une telle suite existe :

    ℤ$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$ ....$\vartriangleright$Gn-1$\vartriangleright${0}

    On se souvient que tous les sous-groupes de ℤ sont de la forme kℤ. Donc il existe un entier k tel que Gn-1=kℤ, mais alors H=2kℤ est un sous-groupe propre (forcément distingué) de Gn-1, et on obtient un raffinement de la suite, ℤ$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$ ....$\vartriangleright$Gn-1$\vartriangleright$H$\vartriangleright${0}contrairement à l'hypothèse.

Quelques théorèmes

Tout groupe fini non trivial admet au moins une suite de Jordan-Hölder

Si G est simple alors G$\vartriangleright${1} est une suite de J-H pour G et c'est la seule. On peut donc supposer que G n'est pas simple.

L'ensemble fini non vide $\mathfrak{H}$ des sous-groupes normaux de G est inductif (toute partie totalement ordonnée est majorée). $\mathfrak{H}$ possède donc un élément maximal H1. Il résulte du lemme précédent que G/H1 est simple. Si H1 est simple alors G$\vartriangleright$H1$\vartriangleright${1} est une suite de J-H pour G et c'est terminé.

Sinon on raisonne par récurrence H1 jouant le rôle de G. On construit ainsi une suite strictement décroissante H1, H2, ...,Hk jusqu'à ce que Hk soit simple ou de cardinal 1.

Alors si Hk={1} on a une suite de J-H :

G$\vartriangleright$H1$\vartriangleright$H2$\vartriangleright$....$\vartriangleright$Hk-1$\vartriangleright${1}

Sinon on a une suite de J-H :

G$\vartriangleright$H1$\vartriangleright$H2$\vartriangleright$....$\vartriangleright$Hk-1$\vartriangleright$Hk$\vartriangleright${1}.
Un groupe abélien admet au moins une suite de J-H si et seulement si il est fini et non trivial.

La proposition précédente établit la démonstration directe.

Pour la réciproque, donnons nous un groupe abélien G admettant une suite de J-H :

G=G0$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$......Gn-1$\vartriangleright$Gn={1}

Pour 0≤i≤n-1 le groupe Gi/Gi+1 est simple, par définition d'une suite de J-H et abélien puisque G l'est. Notons pi+1=|Gi/Gi+1|=[Gi:Gi+1] (revoir au besoin cette définition).

Nous avons alors, [G:G1]=p1 et [G1:G2]=p2. Alors, utilisant ce résultat il vient :

[G:G2]=p1×p2

et par récurrence :

|G|=[G:Gn]=p1×p2×...×pn

G est donc fini.

Caractérisation de la résolubilité par les suites de Jordan-Hölder

Soit G un groupe fini non trivial. Le groupe G est résoluble ssi il existe une suite de J-H à quotients d'ordres premiers (donc cycliques).

Supposons qu'il existe une suite de J-H à quotients premiers (donc cycliques, donc commutatifs). La résolubilité de G résulte alors de ce théorème.

Réciproquement si G est fini, il résulte de cette proposition que G possède une suite de J-H : G=G0$\vartriangleright$G1$\vartriangleright$...$\vartriangleright$Gn={1}. Donc pour tout i 0≤i≤n-1 le quotient Gi/Gi+1 est simple. Alors d'après cette proposition chaque Gi est résoluble et, d'après cette autre, chaque quotient Gi/Gi+1 est résoluble.

Ainsi les quotients Gi/Gi+1 sont simples et résolubles donc cycliques d'après l'exemple 2 de cette page.

Le théorème de Jordan-Hölder

Définition

Deux suites de composition :

G=G0$\vartriangleright$G1$\vartriangleright$G2$\vartriangleright$......Gn-1$\vartriangleright$Gn={1}

G=K0$\vartriangleright$K1$\vartriangleright$K2$\vartriangleright$......Kn-1$\vartriangleright$Kp={1}

sont dites 'équivalentes' lorsque n=p et qu'il existe une permutation σ∈Sn telle que Gi/Gi+1≅Kσ(i)/Kσ(i+1) pour tout 0≤i≤n-1

Exemple

Reprenons l'exemple 3

Suites Quotients
G$\vartriangleright$C12$\vartriangleright$C6$\vartriangleright$C3$\vartriangleright${1} C2,C2,C2,C3
G$\vartriangleright$C12$\vartriangleright$C4$\vartriangleright$C2$\vartriangleright${1} C2,C3,C2,C2
G$\vartriangleright$C12$\vartriangleright$C6$\vartriangleright$C2$\vartriangleright${1} C2,C2,C3,C2
G$\vartriangleright$C8$\vartriangleright$C4$\vartriangleright$C2$\vartriangleright${1} C3,C2,C2,C2

Avec la convention de notation Ck=ℤ/kℤ.

Énonce du théorème

Si G est un groupe admettant une suite de Jordan-Hölder, alors toutes les suites de J-H de G sont équivalentes au sens précédent.

La démonstration de ce théorème, longue, technique exigeant plusieurs lemmes non évidents, dépasse le cadre de cet ouvrage, elle peut se trouver dans la documentation papier : Par exemple S. Lang 'Algebra' pages 102 à 105 ou Bourbaki 1970, p. I.41.

On trouve également des démonstrations sur le web par exemple : Wikiversité